In sailing, rock climbing, construction, and any activity requiring the securing of ropes, certain knots are known to be stronger than others. Any seasoned sailor knows, for instance, that one type of knot will secure a sheet to a headsail, while another is better for hitching a boat to a piling.
But what exactly makes one knot more stable than another has not been well-understood, until now.
MIT mathematicians and engineers have developed a mathematical model that predicts how stable a knot is, based on several key properties, including the number of crossings involved and the direction in which the rope segments twist as the knot is pulled tight.
“These subtle differences between knots critically determine whether a knot is strong or not,” says Jörn Dunkel, associate professor of mathematics at MIT. “With this model, you should be able to look at two knots that are almost identical, and be able to say which is the better one.”
“Empirical knowledge refined over centuries has crystallized out what the best knots are,” adds Mathias Kolle, the Rockwell International Career Development Associate Professor at MIT. “And now the model shows why.”
Dunkel, Kolle, and PhD students Vishal Patil and Joseph Sandt have published their results today in the journal Science.
Pressure’s color
In 2018, Kolle’s group engineered stretchable fibers that change color in response to strain or pressure. The researchers showed that when they pulled on a fiber, its hue changed from one color of the rainbow to another, particularly in areas that experienced the greatest stress or pressure.

An example of overhand knots.
Kolle, an associate professor of mechanical engineering, was invited by MIT’s math department to give a talk on the fibers. Dunkel was in the audience and began to cook up an idea: What if the pressure-sensing fibers could be used to study the stability in knots?
Mathematicians have long been intrigued by knots, so much so that physical knots have inspired an entire subfield of topology known as knot theory — the study of theoretical knots whose ends, unlike actual knots, are joined to form a continuous pattern. In knot theory, mathematicians seek to describe a knot in mathematical terms, along with all the ways that it can be twisted or deformed while still retaining its topology, or general geometry.
“In mathematical knot theory, you throw everything out that’s related to mechanics,” Dunkel says. “You don’t care about whether you have a stiff versus soft fiber — it’s the same knot from a mathematician’s point of view. But we wanted to see if we could add something to the mathematical modeling of knots that accounts for their mechanical properties, to be able to say why one knot is stronger than another.”
Spaghetti physics
Dunkel and Kolle teamed up to identify what determines a knot’s stability. The team first used Kolle’s fibers to tie a variety of knots, including the trefoil and figure-eight knots — configurations that were familiar to Kolle, who is an avid sailor, and to rock-climbing members of Dunkel’s group. They photographed each fiber, noting where and when the fiber changed color, along with the force that was applied to the fiber as it was pulled tight.
The researchers used the data from these experiments to calibrate a model that Dunkel’s group previously implemented to describe another type of fiber: spaghetti. In that model, Patil and Dunkel described the behavior of spaghetti and other flexible, rope-like structures by treating each strand as a chain of small, discrete, spring-connected beads. The way each spring bends and deforms can be calculated based on the force that is applied to each individual spring.
Kolle’s student Joseph Sandt had previously drawn up a color map based on experiments with the fibers, which correlates a fiber’s color with a given pressure applied to that fiber. Patil and Dunkel incorporated this color map into their spaghetti model, then used the model to simulate the same knots that the researchers had tied physically using the fibers. When they compared the knots in the experiments with those in the simulations, they found the pattern of colors in both were virtually the same — a sign that the model was accurately simulating the distribution of stress in knots.
With confidence in their model, Patil then simulated more complicated knots, taking note of which knots experienced more pressure and were therefore stronger than other knots. Once they categorized knots based on their relative strength, Patil and Dunkel looked for an explanation for why certain knots were stronger than others. To do this, they drew up simple diagrams for the well-known granny, reef, thief, and grief knots, along with more complicated ones, such as the carrick, zeppelin, and Alpine butterfly.
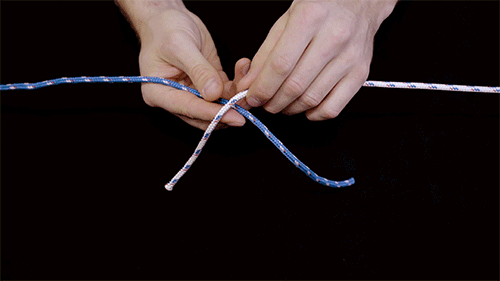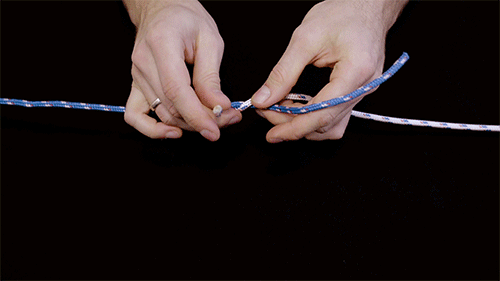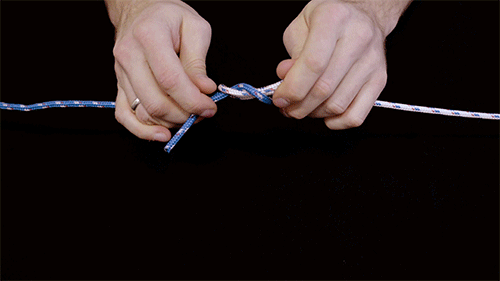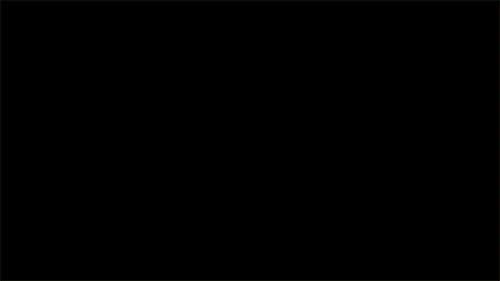
An example of a reef knot.
Each knot diagram depicts the pattern of the two strands in a knot before it is pulled tight. The researchers included the direction of each segment of a strand as it is pulled, along with where strands cross. They also noted the direction each segment of a strand rotates as a knot is tightened.
In comparing the diagrams of knots of various strengths, the researchers were able to identify general “counting rules,” or characteristics that determine a knot’s stability. Basically, a knot is stronger if it has more strand crossings, as well as more “twist fluctuations” — changes in the direction of rotation from one strand segment to another.
For instance, if a fiber segment is rotated to the left at one crossing and rotated to the right at a neighboring crossing as a knot is pulled tight, this creates a twist fluctuation and thus opposing friction, which adds stability to a knot. If, however, the segment is rotated in the same direction at two neighboring crossing, there is no twist fluctuation, and the strand is more likely to rotate and slip, producing a weaker knot.
They also found that a knot can be made stronger if it has more “circulations,” which they define as a region in a knot where two parallel strands loop against each other in opposite directions, like a circular flow.
By taking into account these simple counting rules, the team was able to explain why a reef knot, for instance, is stronger than a granny knot. While the two are almost identical, the reef knot has a higher number of twist fluctuations, making it a more stable configuration. Likewise, the zeppelin knot, because of its slightly higher circulations and twist fluctuations, is stronger, though possibly harder to untie, than the Alpine butterfly — a knot that is commonly used in climbing.
“If you take a family of similar knots from which empirical knowledge singles one out as “the best,” now we can say why it might deserve this distinction,” says Kolle, who envisions the new model can be used to configure knots of various strengths to suit particular applications. “We can play knots against each other for uses in suturing, sailing, climbing, and construction. It’s wonderful.”
This research was supported, in par,t by the Alfred P. Sloan Foundation, the James S. McDonnell Foundation, the Gillian Reny Stepping Strong Center for Trauma Innovation at Brigham and Women’s Hospital, and the National Science Foundation












