A team led by Andrew Sutherland of MIT and Andrew Booker of Bristol University has solved the final piece of a famous 65-year old math puzzle with an answer for the most elusive number of all: 42.
The number 42 is especially significant to fans of science fiction novelist Douglas Adams’ “The Hitchhiker’s Guide to the Galaxy,” because that number is the answer given by a supercomputer to “the Ultimate Question of Life, the Universe, and Everything.”
Booker also wanted to know the answer to 42. That is, are there three cubes whose sum is 42?
This sum of three cubes puzzle, first set in 1954 at the University of Cambridge and known as the Diophantine Equation x3+y3+z3=k, challenged mathematicians to find solutions for numbers 1-100. With smaller numbers, this type of equation is easier to solve: for example, 29 could be written as 33 + 13 + 13, while 32 is unsolvable. All were eventually solved, or proved unsolvable, using various techniques and supercomputers, except for two numbers: 33 and 42.
Booker devised an ingenious algorithm and spent weeks on his university’s supercomputer when he recently came up with a solution for 33. But when he turned to solve for 42, Booker found that the computing needed was an order of magnitude higher and might be beyond his supercomputer’s capability. Booker says he received many offers of help to find the answer, but instead he turned to his friend Andrew "Drew" Sutherland, a principal research scientist in the Department of Mathematics. “He’s a world’s expert at this sort of thing,” Booker says.
Sutherland, whose specialty includes massively parallel computations, broke the record in 2017 for the largest Compute Engine cluster, with 580,000 cores on Preemptible Virtual Machines, the largest known high-performance computing cluster to run in the public cloud.
Like other computational number theorists who work in arithmetic geometry, he was aware of the “sum of three cubes” problem. And the two had worked together before, helping to build the L-functions and Modular Forms Database (LMFDB), an online atlas of mathematical objects related to what is known as the Langlands Program. “I was thrilled when Andy asked me to join him on this project,” says Sutherland.
Booker and Sutherland discussed the algorithmic strategy to be used in the search for a solution to 42. As Booker found with his solution to 33, they knew they didn’t have to resort to trying all of the possibilities for x, y, and z.
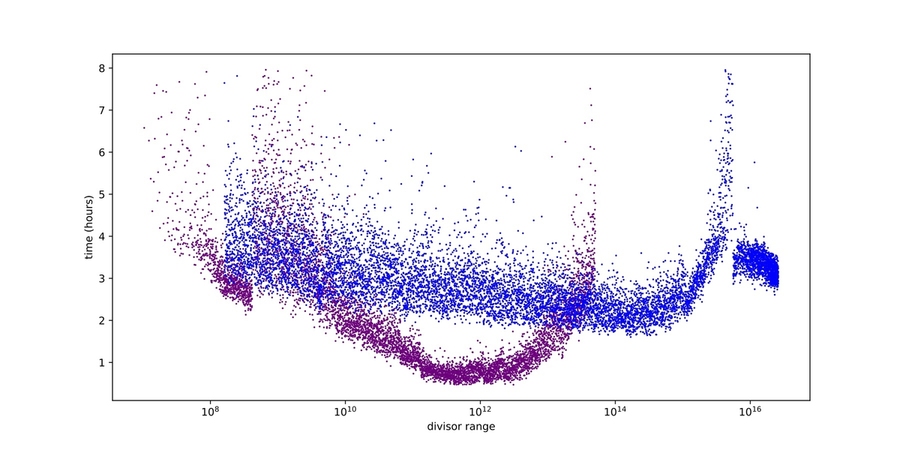
“There is a single integer parameter, d, that determines a relatively small set of possibilities for x, y, and z such that the absolute value of z is below a chosen search bound B,” says Sutherland. “One then enumerates values for d and checks each of the possible x, y, z associated to d. In the attempt to crack 33, the search bound B was 1016, but this B turned out to be too small to crack 42; we instead used B = 1017 (1017 is 100 million billion).
Otherwise, the main difference between the search for 33 and the search for 42 would be the size of the search and the computer platform used. Thanks to a generous offer from UK-based Charity Engine, Booker and Sutherland were able to tap into the computing power from over 400,000 volunteers’ home PCs, all around the world, each of which was assigned a range of values for d. The computation on each PC runs in the background so the owner can still use their PC for other tasks.
Sutherland is also a fan of Douglas Adams, so the project was irresistible.
The method of using Charity Engine is similar to part of the plot surrounding the number 42 in the "Hitchhiker" novel: After Deep Thought’s answer of 42 proves unsatisfying to the scientists, who don’t know the question it is meant to answer, the supercomputer decides to compute the Ultimate Question by building a supercomputer powered by Earth … in other words, employing a worldwide massively parallel computation platform.
“This is another reason I really liked running this computation on Charity Engine — we actually did use a planetary-scale computer to settle a longstanding open question whose answer is 42.”
They ran a number of computations at a lower capacity to test both their code and the Charity Engine network. They then used a number of optimizations and adaptations to make the code better suited for a massively distributed computation, compared to a computation run on a single supercomputer, says Sutherland.
Why couldn't Bristol's supercomputer solve this problem?
“Well, any computer *can* solve the problem, provided you are willing to wait long enough, but with roughly half a million PCs working on the problem in parallel (each with multiple cores), we were able to complete the computation much more quickly than we could have using the Bristol machine (or any of the machines here at MIT),” says Sutherland.
Using the Charity Engine network is also more energy-efficient. “For the most part, we are using computational resources that would otherwise go to waste,” says Sutherland. “When you're sitting at your computer reading an email or working on a spreadsheet, you are using only a tiny fraction of the CPU resource available, and the Charity Engine application, which is based on the Berkeley Open Infrastructure for Network Computing (BOINC), takes advantage of this. As a result, the carbon footprint of this computation — related to the electricity our computations caused the PCs in the network to use above and beyond what they would have used, in any case — is lower than it would have been if we had used a supercomputer.”
Sutherland and Booker ran the computations over several months, but the final successful run was completed in just a few weeks. When the email from Charity Engine arrived, it provided the first solution to x3+y3+z3=42:
42 = (-80538738812075974)^3 + 80435758145817515^3 + 12602123297335631^3
“When I heard the news, it was definitely a fist-pump moment,” says Sutherland. “With these large-scale computations you pour a lot of time and energy into optimizing the implementation, tweaking the parameters, and then testing and retesting the code over weeks and months, never really knowing if all the effort is going to pay off, so it is extremely satisfying when it does.”
Booker and Sutherland say there are 10 more numbers, from 101-1000, left to be solved, with the next number being 114.
But both are more interested in a simpler but computationally more challenging puzzle: whether there are more answers for the sum of three cubes for 3.
“There are four very easy solutions that were known to the mathematician Louis J. Mordell, who famously wrote in 1953, ‘I do not know anything about the integer solutions of x3 + y3 + z3 = 3 beyond the existence of the four triples (1, 1, 1), (4, 4, -5), (4, -5, 4), (-5, 4, 4); and it must be very difficult indeed to find out anything about any other solutions.’ This quote motivated a lot of the interest in the sum of three cubes problem, and the case k=3 in particular. While it is conjectured that there should be infinitely many solutions, despite more than 65 years of searching we know only the easy solutions that were already known to Mordell. It would be very exciting to find another solution for k=3.”