Animators could create more realistic bouncy, stretchy, and squishy characters for movies and video games thanks to a new simulation method developed by researchers at MIT.
Their approach allows animators to simulate rubbery and elastic materials in a way that preserves the physical properties of the material and avoids pitfalls like instability.
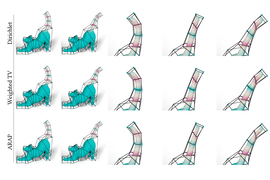
The technique simulates elastic objects for animation and other applications, with improved reliability compared to other methods. In comparison, many existing simulation techniques can produce elastic animations that become erratic or sluggish or can even break down entirely.
To achieve this improvement, the MIT researchers uncovered a hidden mathematical structure in equations that capture how elastic materials deform on a computer. By leveraging this property, known as convexity, they designed a method that consistently produces accurate, physically faithful simulations.

Image: Courtesy of the researchers
“The way animations look often depends on how accurately we simulate the physics of the problem,” says Leticia Mattos Da Silva, an MIT graduate student and lead author of a paper on this research. “Our method aims to stay true to physical laws while giving more control and stability to animation artists.”
Beyond 3D animation, the researchers also see potential future uses in the design of real elastic objects, such as flexible shoes, garments, or toys. The method could be extended to help engineers explore how stretchy objects will perform before they are built.
She is joined on the paper by Silvia Sellán, an assistant professor of computer science at Columbia University; Natalia Pacheco-Tallaj, an MIT graduate student; and senior author Justin Solomon, an associate professor in the MIT Department of Electrical Engineering and Computer Science and leader of the Geometric Data Processing Group in the Computer Science and Artificial Intelligence Laboratory (CSAIL). The research will be presented at the SIGGRAPH conference.
Truthful to physics
If you drop a rubber ball on a wooden floor, it bounces back up. Viewers expect to see the same behavior in an animated world, but recreating such dynamics convincingly can be difficult. Many existing techniques simulate elastic objects using fast solvers that trade physical realism for speed, which can result in excessive energy loss or even simulation failure.
More accurate approaches, including a class of techniques called variational integrators, preserve the physical properties of the object, such as its total energy or momentum, and, in this way, mimic real-world behavior more closely. But these methods are often unreliable because they depend on complex equations that are hard to solve efficiently.
The MIT researchers tackled this problem by rewriting the equations of variational integrators to reveal a hidden convex structure. They broke the deformation of elastic materials into a stretch component and a rotation component, and found that the stretch portion forms a convex problem that is well-suited for stable optimization algorithms.
“If you just look at the original formulation, it seems fully non-convex. But because we can rewrite it so that is convex in at least some of its variables, we can inherit some advantages of convex optimization algorithms,” she says.
These convex optimization algorithms, when applied under the right conditions, come with guarantees of convergence, meaning they are more likely to find the correct answer to the problem. This generates more stable simulations over time, avoiding issues like a bouncing rubber ball losing too much energy or exploding mid-animation.
One of the biggest challenges the researchers faced was reinterpreting the formulation so they could extract that hidden convexity. Some other works explored hidden convexity in static problems, but it was not clear whether the structures remained solid for dynamic problems like simulating elastic objects in motion, Mattos Da Silva says.
Stability and efficiency
In experiments, their solver was able to simulate a wide range of elastic behavior, from bouncing shapes to squishy characters, with preservation of important physical properties and stability over long periods of time. Other simulation methods quickly ran into trouble: Some became unstable, causing erratic behavior, while others showed visible damping.

Image: Courtesy of the researchers
“Because our method demonstrates more stability, it can give animators more reliability and confidence when simulating anything elastic, whether it’s something from the real world or even something completely imaginary,” she says.
While the solver is not as fast as some simulation tools that prioritize speed over accuracy, it avoids many of the trade-offs those methods make. Compared to other physics-based approaches, it also avoids the need for complex, nonlinear solvers that can be sensitive and prone to failure.
In the future, the researchers want to explore techniques to further reduce computational cost. In addition, they want to explore applications of this technique in fabrication and engineering, where reliable simulations of elastic materials could support the design of real-world objects, like garments and toys.
“We were able to revive an old class of integrators in our work. My guess is there are other examples where researchers can revisit a problem to find a hidden convexity structure that could offer a lot of advantages,” she says.
This research is funded, in part, by a MathWorks Engineering Fellowship, the Army Research Office, the National Science Foundation, the CSAIL Future of Data Program, the MIT-IBM Watson AI Laboratory, the Wistron Corporation, and the Toyota-CSAIL Joint Research Center.