For more than a decade, gene sequencers have been improving more rapidly than the computers required to make sense of their outputs. Searching for DNA sequences in existing genomic databases can already take hours, and the problem is likely to get worse.
Recently, Bonnie Berger’s group at MIT’s Computer Science and Artificial Intelligence Laboratory (CSAIL) has been investigating techniques to make biological and chemical data easier to analyze by, in some sense, compressing it.
In the latest issue of the journal Cell Systems, Berger and colleagues present a theoretical analysis that demonstrates why their previous compression schemes have been so successful. They identify properties of data sets that make them amenable to compression and present an algorithm for determining whether a given data set has those properties. They also show that several existing databases of chemical compounds and biological molecules do indeed exhibit them.
Given measurements for those properties, the researchers can also calculate the improvements in search efficiency that their compression techniques afford. For the data sets they analyze, those efficiencies scale sublinearly, meaning that the larger the data set, the more efficient the search should be.
“This paper provides a framework for how we can apply compressive algorithms to large-scale biological data,” says Berger, a professor of applied mathematics at MIT. “We also have proofs for how much efficiency we can get.”
The key to the researchers’ compression scheme is that evolution is stingy with good designs. There tends to be a lot of redundancy in the genomes of closely related — or even distantly related — organisms.
That means that of all the possible sequences of the four DNA letters — A, T, C, and G — only a very small subset is represented by the genomes of real organisms. Moreover, within the space of possible genomes, those of real organisms are not distributed randomly. Instead, they trace out continuous patterns, which represent the relatively slow rate at which species diverge.
Birds of a feather
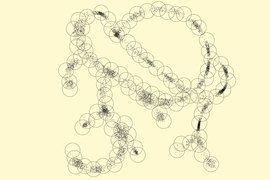
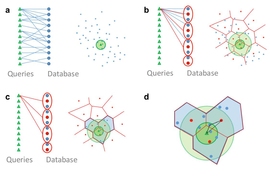
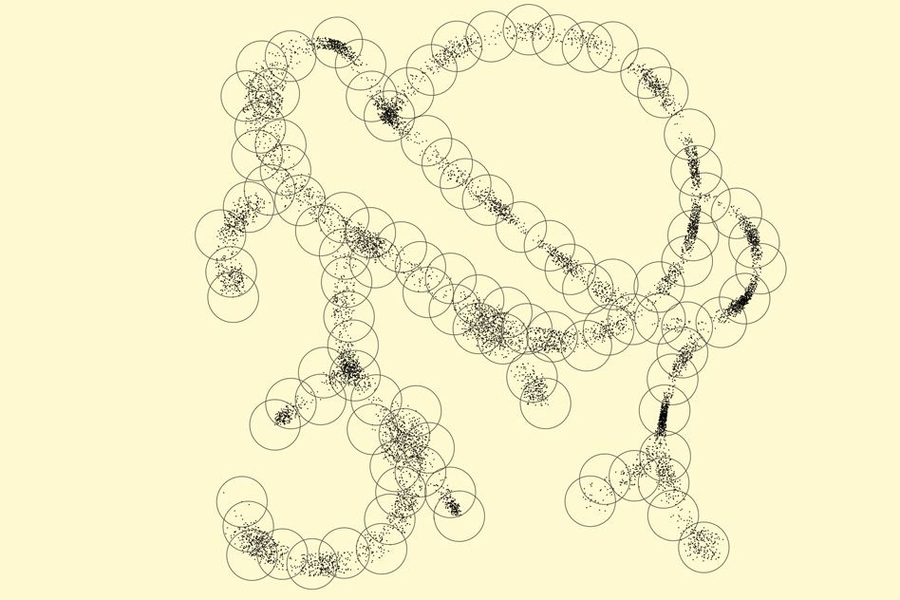
To make searching more efficient, the Berger group’s compression algorithms cluster together similar genomic sequences — those that diverge by only a few DNA letters —then choose one sequence as representative of the cluster. A search can concentrate only on the likeliest clusters; most of the data never has to be examined.
If genomic data is envisioned as tracing a continuous path through a much larger space of possibilities, then the clusters can be envisioned as spheres superimposed on the data. Data points that fall within a single sphere are closely related.
Berger and her colleagues — first authors Noah Daniels, a postdoc in her group, and William Yu, a graduate student in applied mathematics, and David Danko, an undergraduate major in computational biology — show that data sets are amenable to their compressive search techniques if they meet two criteria. The first they refer to as metric entropy. This means that the data inhabits only a small part of the larger space of possibilities.
The second is low fractal dimension. That means that the density of the data points doesn’t vary greatly as you move through the data. If your search requires you to explore three spheres rather than one, it takes only three times as long — not 10 times, or 100 times.
In their paper, the MIT researchers analyze three data sets. Two describe proteins — one according to their sequences of amino acids, the other according to their shape — and the third describes organic molecules. In a separate paper, now under submission, the researchers apply the same types of analysis to DNA segments between 32 and 63 letters in length.
Time’s arrow
The efficiency of their search algorithm scales sublinearly, not with the number of data points, but with the metric entropy of the data set, which is a formal measure of the continuity of the data and their sparseness, relative to the space of possibilities. Because evolution is conservative, the metric entropy of genomic data should increase as new genomes are sequenced. That is, the addition of new genomes will not, in all likelihood, add new branches to the pattern traced out in the space of possibilities; rather, it will fill in gaps in the existing pattern, increasing the metric entropy.
Many other large data sets, however, could prove to be conservative in the same way. The range of behaviors exhibited by Web users, for instance, may, relative to the entire space of possibilities, be constrained by biology, by cultural history, or both. The MIT researchers’ compression techniques could thus be applicable to a wide range of data outside biology.
“The authors show that the local structure of genomics data can be exploited to speed up matching, by adopting a conceptually simple strategy,” says Lior Pachter, a professor at the University of California at Berkeley, whose appointments span the departments of mathematics, molecular and cell biology, and electrical engineering and computer science. “In empirical studies, they show via a number of examples that their strategy works. Moreover, they show that even a naive and simple approach to the hardest problem in the approach — finding the clusters — works well.”
“In my view, one interesting implication of the work that could be explored in future papers is the use of the coverings they produce to study the inherent structure of ‘omics’ data more carefully,” Pachter adds. “This may have applications not only to search but also to exploratory data analysis and statistical inference.”