For the first time, MIT chemists have measured the energy of the transition state of a chemical reaction — a fleeting, unstable state that is a reaction’s point of no return.
Chemists have long believed it impossible to experimentally characterize transition states, but the MIT team achieved it by analyzing changes in the patterns of vibrational energy levels in reactants approaching the transition state.
“This was supposed to be impossible because of the intrinsic complexity, but we found the magic decoder that enables us to go deeper into this regime,” says Robert Field, the Robert T. Haslam and Bradley Dewey Professor of Chemistry and senior author of the study, which appears in the Dec. 10 online edition of Science.
Broken patterns
As every freshman chemistry student learns, the transition state of a reaction is the gateway between reactants and products. Most reactions require an input of energy, known as the activation energy, to reach the transition state.
“Your reactants and products are stable valleys on either side of a mountain range, and the transition state is the pass. It’s the most convenient way to get from one to the other,” says Josh Baraban, the paper’s lead author and a former MIT graduate student who is now a research associate at the University of Colorado Boulder. “Because it only exists as you go from as one thing to another, it’s never really been thought of as something that you can easily study directly.”
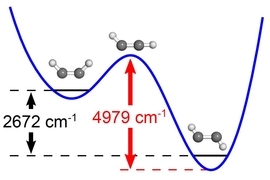
Field, Baraban, and their colleagues investigated a type of reaction known as an isomerization, in which a molecule undergoes a change of shape. They focused on acetylene, a molecule consisting of two carbon atoms bound to each other, each with one hydrogen atom attached to it. Field’s lab has long studied the isomerization of the most stable linear form of acetylene to an isomer called vinylidene.
In this work, which focused on an excited electronic state of acetylene, the molecule converts from a U-shaped conformation, in which both hydrogen atoms are above the carbon-carbon bond, to a zigzag conformation, in which one hydrogen atom is above and the other is below.
The MIT team used tunable laser spectroscopy to monitor changes in the vibrations of the acetylene molecules as the researchers added more energy to the system. Ordinarily, molecules vibrate at frequencies that evolve in a predictable pattern with increasing energy. From these patterns, the researchers can infer the vibrational motion of the molecules at each energy level.
As the researchers systematically explored increasing energy levels, they observed the predicted patterns until the molecules reached a certain and carefully chosen internal energy arrangement. At this point the patterns broke down and the molecules exhibited vibrations at significantly lower frequencies than expected.
“We realized that where we saw the patterns breaking specifically involved the vibrations that were related to the kind of structural changes that should be happening” at the transition state between these two conformations, Baraban says. “It looks exactly like what you’d expect.”
“This is a major breakthrough in our ability to understand how chemical transformations happen,” says Richard Zare, a professor of chemistry at Stanford University who was not involved in the research. “By examining the frequency spacing between different vibrational oscillations, Field and co-workers can tell which vibrations play an active role in molecular contortions and which vibrations are inactive, being merely passive bystanders to the spatial rearrangement of the atoms in a molecule that change their positions during isomerization.”
The researchers also devised a formula that allows them to determine the energy of the transition state. This result is important for predictions based on the Arrhenius equation, which describes how temperature affects chemical reaction rates.
Other reactions
In this study, the team also used this technique to accurately predict the transition-state structure and energy of the isomerization of hydrogen cyanide (HCN) to hydrogen isocyanide (HNC). When this happens, a hydrogen atom originally bound to carbon gets passed to nitrogen.
Although they focused on isomerization reactions in this study, the researchers believe that this approach could in principle also be applied to any other reaction that must overcome an energy barrier. Analyzing complex reactions such as those where two molecules come together or one molecule breaks into two should be possible but would be more technically challenging, they say.
Other authors of the Science paper are former MIT undergraduate Bryan Changala; Georg Mellau, a professor at Justus Liebig University Giessen in Germany; John Stanton, a professor at the University of Texas at Austin; and Anthony Merer, a professor at the University of British Columbia and the Institute for Atomic and Molecular Science in Taiwan.